 |
| Fuente: https://orientacionsanvicente.files.wordpress.com/2012/05/imagen-1.png |
Resolución de problemas n° 3.
Para efectos de ilustración
sobre conceptos previos relacionados con la resolución de problemas matemáticos
y solución del problema n° 1, accédase a los mismos al seguir este enlace:
Solución.
Para resolver este problema, los conceptos
fundamentales previos son: decenas, unidades, sistemas de numeración y
conversión de un número dado en un sistema de numeración al sistema de
numeración decimal, entre otros.
a) El problema
propuesto aunque parezca absurdo, insólito e incluso sin solución, puede ser
resuelto si se recurre a las ecuaciones lineales de primer grado con una
incógnita.
b)
El lector perspicaz y que haya
aprovechado sus clases de Matemática, podrá comprender que los datos del
problema no corresponden al sistema decimal; por cuanto la pregunta propuesta, sería absurda.
c)
Suponga que la base del sistema de numeración desconocido es x;
entonces, el número “84” equivale a 8 unidades de segundo orden y 4 de unidades
de primer orden, del sistema decimal; esto es:
d)
Luego, aplicando el mismo razonamiento, se tiene que:
e)
Entonces, es posible obtener la ecuación
para el cálculo de la base desconocida:
f) Al resolver la ecuación (**), se obtiene que x = 12; i.e. la base del sistema de
numeración desconocido es 12.
g) Así, al sustituir x = 12 en la ecuación (*), se tiene que:
h) Conclusión:
La
equivalencia de 84 (en base 12) es igual a 100 (en base10):
NOTA. Ahora que ya sabe resolver este
tipo de problemas, resuelva estos otros.
Bibliografía.
Perelman, Y. I. (1985). ÁLGEBRA RECREATIVA. (C.
y. Pérez, Trad.) México, D.F.: Ediciones de Cultura Popular, S.A., pág. 72.

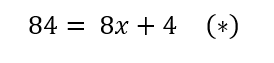






Comentarios